We already saw how the GLSL (that's the OpenGL Shader Language) built-in function "length" can be used to calculate the distance of a point from the centre (0,0) - great for making circles.
GLSL has many other built in functions. Lets use a couple of those to make squarish shapes.:
vec2 r=abs(c.xy);
f=vec4(r,0.,1.)
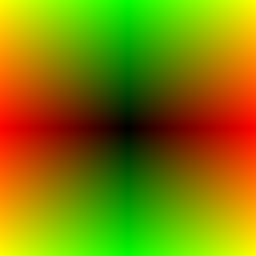
The abs function makes negative numbers positive - it reflects them around zero. Since our c coordinate is negative to the left and top, taking the abs of it and setting the red to c.x, and green to c.y, gives a symmetrical image around the centre.:
vec2 r=abs(c.xy);
float s=max(r.x,r.y);
f=vec4(vec3(s),1.)

Now we inserted a max function. This takes two arguments, and returns the largest one for each element. In this case it returns either r.x or r.y, depending on which is larger.
This gives us an interesting and useful <b>distance field</b>. In this field, the value gives the distance of that point from the nearest point on the nearest edge of a square.
The simple length(c.xy) distance field we made previously was useful for giving us different sized circles. This one can give us different kinds of squares:
vec2 r=abs(c.xy);
float s=step(.5,max(r.x,r.y));
f=vec4(vec3(s),1.)
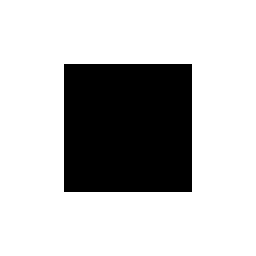
As with the circular distance field, a step function changes the field to a solid square shape. By changing the threshold value for the step, we can make larger or smaller squares.
But we don't have to limit ourselves to solid squares:
vec2 r=abs(c.xy);
float s=max(r.x,r.y);
f=vec4(vec3(step(.4,s)* step(s,.5)),1.)

By multiplying two step functions with reversed argument orders and different thresholds, we can make a hard edge which is as wide as we like.
Now if we change from using step to using smoothstep, we can make the edge softer:
vec2 r=abs(c.xy);
float s=max(r.x,r.y);
f=vec4(vec3(smoothstep(.3,.4,s)* smoothstep(.6,.5,s)),1.)

If you are looking for something slightly less square, then we need a different distance field, like this one.
This time we subtract an offset - in this case 0.3 - from the abs, and then take the max of that and zero before taking the length of the result:
vec2 r=length(max( abs(c.xy)-.3,0.));
f=vec4(r,r,r,1.)

<p>As you can see, this again gives a square in the middle with size determined by the offset amount. But now the field near the corners is curved instead of straight.
You can probably guess already what shape we will get when we apply a step function.:
vec2 r=step(.2, length(max(abs(c.xy)-.3,0.)));
f=vec4(r,r,r,1.)

Yes, it's a square with rounded corners. By tweaking the step threshold you can get more or less roundedness. The pair of steps from earlier could also be used to give a round edged border.
Finally lets try yet another way to create a square. This one is a bit more expensive because it's based on angles. First we find the angle of each point using the atan function.
Then we scale the angle to be in the range -1.5 to 2.5 and then round it down to the nearest integer using the floor function. This puts each point into one of four quadrants.
We then turn that back into an angle and subtract the difference between that and the actual angle. Taking cos of that difference and multiplying by the length of the original point gives the distance of that point along the vector for the centre line of the quadrant. Finally a step turns that into a square. Phew.:
float a=atan(c.x,c.y);
f=vec4(step(.5,cos( floor(a*.636+.5)* 1.57-a)*length(c.xy)))
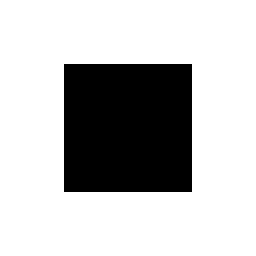
The nice thing about this approach is that with a different scale factor, it can give us ANY regular polygon, not just a square. It's also easy to rotate with an offset to the angle.
Here is a parameterised version (from @srodal) which defaults to a 7-side heptagon.:
int N=7;
float a=atan(c.x,c.y)+.2;
float b=6.28319/float(N);
f=vec4(vec3(smoothstep(.5,.51, cos(floor(.5+a/b)*b-a)*length(c.xy))),1.);

These basic techniques start to open up all kinds of possibilities for constructing more interesting and useful images just using shaders.